Μεθοδολογία
υπολογισμού μεταβολής
θέσης στα αποτελέσματα
της Google
Από γεννήσεως του SEO υπήρχε το πρόβλημα της συνολικής απεικόνισης της μεταβολής της θέσης μιας ιστοσελίδας στα αποτελέσματα της Google για ένα σύνολο ερωτημάτων (λέξεων-κλειδιών). Πώς μπορούμε να παρουσιάσουμε το μέσο όρο της αύξησης ή της μείωσης για ένα σύνολο λέξεων-κλειδιών, οι οποίες όμως έχουν διαφορετική βαρύτητα.
Πρώτος παράγοντας:
Η σελίδα αποτελεσμάτων
Το πρόβλημα
H βαρύτητα που έχει η μεταβολή μιας λέξης κλειδί από τη θέση 12 στη θέση 8 είναι πολύ σημαντικότερη από μια μεταβολή από τη θέση 76 στην θέση 72, παρόλο που και οι δύο μεταβολές έχουν διαφορά 4 θέσεις. Σε ένα σύνολο λέξεων κλειδιών που μεταβλήθηκαν διαφορετικά σε ίδιες χρονικές περιόδους, για να υπολογισθεί ο μέσος όρος πρέπει να συνυπολογιστεί και ο παράγοντας της τελικής θέσης κατάταξης.Η λύση
Για τον υπολογισμό του μέσου όρου μεταβολής στη θέση κατάταξης ενός συνόλου λέξεων κλειδιών, που λαμβάνεται ο παράγοντας της τελικής θέσης μπορούμε να ορίσουμε συντελεστές βαρύτητας. Για παράδειγμα όταν η τελική θέση είναι στην πρώτη σελίδα αποτελεσμάτων της google (δηλαδή θέσεις από 1-10) μπορούμε να ορίσουμε τον συντελεστή βαρύτητας 1,50, στη δεύτερη σελίδα 1,00 (θέσεις 10-20) και στην τρίτη 0,50 (θέσεις 20-30). Για την μεταβολή της λέξης1 από την θέση 22 στην θέση 19 η πραγματική μεταβολή είναι 32-29=3 αλλά με συνυπολογίζοντας τον συντελεστή βαρύτητας είναι (22-19)*0,5=1,5Τυπολόγιο
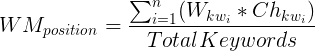
ή πιό απλά
όπου
WMposition = σταθμισμένος μέσος όρος
Wkw1 = συντελεστής βαρύτητας, λέξης1
Chkw1 = η μεταβολή της θέσης κλειδί1 μεταξύ δύο ημερομηνιών
Παράδειγμα
Υπολογισμού μέσου όρου με συντελεστές βαρύτητας την θέση (σταθμισμένος μέσος όρος)
Έχουμε τις ακόλουθες μεταβολές:
Λέξη1 από θέση 43 σε 38 (+5)
Λέξη2 από θέση 12 σε 8 (+4)
Λέξη3 από θέση 7 σε 16 (-9)
Λέξη4 από θέση 22 σε 36 (-14)
Και συντελεστές βαρύτητας:
Σελίδα 1 (αποτελέσματα 1-10) = 1,5
Σελίδα 2 (αποτελέσματα 11-20) = 1,0
Σελίδα 3 (αποτελέσματα 21-30) = 0,5
Σελίδα 4+ (αποτελέσματα 31+) = 0,2
Οπότε οι συντελεστές βαρύτητας διαμορφώνονται:
Για τη λέξη1 που πήγε στη 4η σελίδα: 0,2
Για τη λέξη2 που πήγε στη 1η σελίδα: 1,5
Για τη λέξη3 που πήγε στη 2η σελίδα: 1,0
Για τη λέξη4 που πήγε στη 4η σελίδα: 0,2
Άρα ο σταθμισμένος μέσος όρος για τον παράγοντα θέση θα είναι:
WMposition = (0,2*5)+(1,5*4)+(0,5*-9)+(0,2*-14) ⁄ 4 =
Δεύτερος παράγοντας:
Ο αριθμός αναζητήσεων
(search volume)
Το πρόβλημα
H βαρύτητα που έχει η μεταβολή μιας λέξης κλειδί που έχει πολύ περισσότερες αναζητήσεις σε σχέση με την ίδια μεταβολή μιας άλλης λέξης κλειδί που δεν έχει αρκετές αναζητήσεις από τους χρήστες, είναι σαφώς πιο σημαντική. Σε ένα σύνολο λέξεων κλειδιών με διαφορετικές μηνιαίες αναζητήσεις από τους χρήστες που μεταβλήθηκαν διαφορετικά σε ίδιες χρονικές περιόδους, για να υπολογισθεί ο μέσος όρος πρέπει να συνυπολογιστεί και ο παράγοντας αυτός.Η λύση
Για τον υπολογισμό του μέσου όρου μεταβολής στη θέση κατάταξης ενός συνόλου λέξεων κλειδιών, που λαμβάνεται ο παράγοντας των μηνιαίων αναζητήσεων μπορούμε να ορίσουμε συντελεστές βαρύτητας, που θα καθορίζονται από τον αριθμό των αναζητήσεων. Έτσι ο αριθμός των αναζητήσεων για κάθε λέξη κλειδί ενός συνόλου λέξεων κλειδιών καθορίζεται αναλογικά. Ο αριθμός αναζητήσεων που έχει μια λέξη δια τον μέσο όρο των αναζητήσεων του συνόλου λέξεων κλειδιών, καθορίζει τον συντελεστή βαρύτητας. Πρέπει να επισημανθεί πως η διαφορά των αναζητήσεων κάθε λέξης κλειδί του συνόλου δεν πρέπει να είναι μεγάλη, γιατί έτσι θα μονοπωλείται η βαρύτητα στο μέσο σταθμισμένο όρο από τις «βαριές» λέξεις. (για παράδειγμα δεν μπορεί η μία λέξη κλειδί να έχει 50000 αναζητήσεις και οι υπόλοιπες κάτω από 100, γιατί έτσι δε θα λαμβάνονται σχεδόν καθόλου στο τελικό αποτέλεσμα)Τυπολόγιο
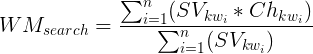
ή πιό απλά
όπου
WMsearch = σταθμισμένος μέσος όρος
SVkw1 = οι μηνιαίες αναζητήσεις της λέξης1
CHkw1 = η μεταβολή της θέσης κλειδί1 μεταξύ δύο ημερομηνιών
TotalSearches = Συνολικός αριθμός αναζητήσεων όλων των λέξεων
Παράδειγμα
Υπολογισμού σταθμισμένου μέσου όρου με συντελεστές βαρύτητας τις αναζητήσεις
Έχουμε τις ακόλουθες μεταβολές:
Λέξη1 από θέση 43 σε 38 (+5)
Λέξη2 από θέση 12 σε 8 (+4)
Λέξη3 από θέση 7 σε 16 (-9)
Λέξη4 από θέση 22 σε 36 (-14)
Έχουμε τις ακόλουθες αναζητήσεις των λέξεων:
Την Λέξη1 την αναζητούν 220 χρήστες
Την Λέξη2 την αναζητούν 150 χρήστες
Την Λέξη3 την αναζητούν 270 χρήστες
Την Λέξη4 την αναζητούν 200 χρήστες
Οπότε το σύνολο των αναζητήσεων είναι 840
Άρα ο σταθμισμένος μέσος όρος για τον παράγοντα αναζητήσεις θα είναι:
WMsearch = (220*5)+(150*4)+(270*-9)+(200*-14) ⁄ 840 =
Συνολικό αποτέλεσμα
λαμβάνοντας υπόψη την σελίδα αποτελεσμάτων και τον αριθμό αναζητήσεων
Φτάσαμε στο σημείο που πρέπει να συμπεριφερθούν και οι δύο παραπάνω παράγοντες για τον υπολογισμό ενός τελικού σταθμισμένου μέσου όρου της μεταβολής του συνόλου λέξεων κλειδιών. Εδώ μπορούμε να υπολογίσουμε τον μέσο των δύο σταθμισμένων μέσων που υπολογίσαμε παραπάνω, εφόσον και οι δύο παράγοντες έχουν την ίδια βαρύτητα.
Εύκολος υπολογισμός με Excel
Επειδή η παραπάνω διαδικασία μπορεί να γίνει περίπλοκη για τον υπολογισμό μεγάλου συνόλου λέξεων κλειδιών και όταν γίνεται μεταξύ πολλαπλών χρονικών περιόδων, έφτιαξα ένα αρχείο excel το οποίο υπολογίζει αυτόματα τους παραπάνω μέσους σταθμισμένους όρους, το τελικό αποτέλεσμα, αλλά και την σταθμισμένη μεταβολή ανά λέξη κλειδί ξεχωριστά.
Κάντε κλίκ εδώ για να κατεβάσετε αυτό το άρθρο/τυπολόγιο σε αρχείο PDF!
Υπολογισμός σταθμισμένου μέσου όρου μεταβολής θέσης στα αποτελέσματα της Google με αρχείο Excel
Με αυτό το αρχείο excel υπολογίστε έυκολα τη συνολική απόδοση της αλλαγής θέσεων ενός συνόλου ερωτημάτων που εμφανίζεται μια ιστοσελίδα, λαμβάνοντας υπόψιν τους παραπάνω παράγοντες και μαθηματικούς τύπους.
Κάντε κλικ εδώ για να το κατεβάσετε!
ή δείτε περισσότερες πληροφορίες
*Ο Μιχάλης Δημητρίου εργάζεται στον τομέα των τυχερών παιχνιδιών (iGaming) και στοιχηματισμού ως υπέυθυνος digital marketing στην εξωτική Μάλτα, ενώ παράλληλα υποστηρίζει εταιρείες SEO σε όλο τον κόσμο για έργα ψηφιακής προώθησης. Επίσης είναι όμορφος, πανέξυπνος και πετυχημένος.
14 Απριλίου 2016
