By Michail Dimitriou*



Since the birth of SEO, there has been the problem of the overall depiction of changing a site's position in Google's results for a set of queries (keywords). How we can present the average increase or decrease for a set of keywords, which however have different gravity.

First Factor:

The results page

The problem

The gravity of changing a keyword from the position 12 to the position 8 is much more important than a change from the position 76 to the position 72, although both changes have a difference of 4 positions. In a set of keywords that were altered differently over the same time periods, in order to find the average position factor we should calculate and the final placement factor.

The solution

In order to calculate the average change in the ranking position of a set of keywords, where the factor of the final position is taken into consideration, we can define gravity coefficients. For example, when the final position is in the first google results page (e.g. positions 1-10), we can define the gravity factor 1.50, the second page 1.00 (positions 10-20) and the third 0.50 Positions 20-30). To change the word1 from the position 22 to the position 19, the real variation is 32-29 = 3, but when taking into account the gravity factor is (22-19) * 0.5 = 1.5

Handbook

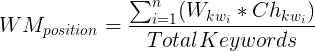
or in simple words



where
WM_position = weighted average
W_kw1 = gravity factor, word1
Ch_kw1 = the alteration of the keyword1 between two dates

Example

Average calculation with position weights (weighted average)

We have the following alterations:
Word1 from the position 43 to 38 (+5)
Word2 from the position 12 to 8 (+4)
Word3 from the position 7 to 16 (-9)
Word4 from the position 22 to 36 (-14)

And the gravity factors:
Page 1 (results 1-10) = 1,5
Page 2 (results 11-20) = 1,0
Page 3 (results 21-30) = 0,5
Page 4+ (results 31+) = 0,2

So the gravity factors are formed:
For the word1 that went to the page 4 : 0,2
For the word2 that went to the page 1 : 1,5
For the word3 that went to the page 2 : 1,0
For the word4 that went to the page 4 : 0,2

So the weighted average for the factor position will be:

WM_position = ^{(0,2*5)+(1,5*4)+(0,5*-9)+(0,2*-14)} ⁄ ₄ =

Second factor:

The number of searches

(search volume)

The problem

The gravity of changing a keyword that has far more searches than the same change of another keyword that does not have enough searches from users is clearly more important. In a set of keywords with different monthly searches from users who changed differently over the same time periods, in order to calculate the average we should also count this factor.

The solution

To calculate the average change in the rank position of a set of keywords, we obtain the factor of the monthly searches we can set weighting factors, which will be determined by the number of searches. Thus, the number of searches for each keyword in a set of words is proportionally determined. The number of searches that has a word for the average of searches for the total of keywords determines the gravity factor. It should be pointed out that the difference between the searches of each keyword of the total should not be big, because then the gravity will be monopolized in the weighted average term by the "heavy" words. (For example, one keyword cannot have 50000 searches and the rest below 100, because in that way they will not be taken under consideration at the final result).

Handbook

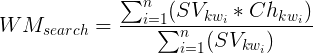
or in simple words



where
WM_search = weighted average
SV_kw1 = the annual searches of the word1
CH_kw1 = the alteration of the position of the key word1 between two dates
TotalSearches = total number of searches of all the words

Example

Calculation of the weighted average with the searches as weigh factors

We have the following alterations:
Word1 from the position 43 to 38 (+5)
Word2 from the position 12 to 8 (+4)
Word3 from the position 7 to 16 (-9)
Word4 from the position 22 to 36 (-14)

We have the following word searches:
The word1 is being searched by 220 users
The word2 is being searched by 150 users
The word3 is being searched by 270 users
The word4 is being searched by 200 users
Thus the total of searches is 840

Thus the weighted average for the factor searches will be:

WM_search = ^{(220*5)+(150*4)+(270*-9)+(200*-14)} ⁄ ₈₄₀ =

Total result

by taking into consideration the results page and the number of searches

We have reached the point where both factors should behave in order to calculate a final weighted average of the change in the total of keywords. Here we can calculate the average of the two weighted averages that we calculated above, since both those two factors have the same gravity.

Easy way to calculate using Excel

Because the above process can be complicated for calculating a large set of keywords, also when it is done between multiple periods of time, I've made an excel file that automatically calculates the above average weighted terms, the final result, and the weighted change per key word separately.

Calculating a weighted average position change in Google results with an Excel file

With this excel file, you can easily calculate the set return position change of a total of queries displayed on a webpage, taking into consideration the above factors and mathematical formulas.

Click here to download it!
or go to more information

*Michail Dimitriou is working in the field of iGaming as a digital marketing executive for an iGaming company in the exotic Malta as well as an SEO freelancer. He supports several advertising companies and digital agencies around the world.
Also he is smart and handsome.


Last Update: 30 June 2017